对于FFT的精度小优化:
对于$PI$,关于预处理单位复数根,
精度差不少,感谢skyh大神的帮助
1 const long double PI=acos(-1.0L); 2 inline void init(const int &lim){ 3 for(int i=1;i<lim;i<<=1) 4 for(int k=0;k<i;++k) 5 omg1[i+k]=Cp(cos(PI*k/i),sin(PI*k/i)); 6 return ; 7 }
只用开一维数组,这种存法自己手模一下还是很清晰的
一种处理图的根号算法:
今天做题一道比较清新的$O(n*sqrt{n})$算法。
好像比较套路的样子。
在这个联通图里要维护一些东西,询问某个点所有连向点对他的贡献这个样子。
因为有些修改,比较难维护,所以貌似只能枚举的类型。
此时可以按点的度数划分使总的枚举次数减少。
具体是设个$lim=sqrt{n}$,把度数大于$lim$的点划分成大点,其次为小点。
然后以今天的题举例。
给定序列,要依次求这个点的相邻点的权值和,然后修改这个点。
可以设一个$sum_{x}$表示所有小点对点$x$的贡献。
每次询问小点贡献直接调用数组,大点枚举。
修改时如果此点为小点,枚举所有边更新$sum$。
可以时间复杂度保证在$O(n*sqrt{n})$
UPD:
$double$小数位,整数位都有可存位数多的特点,但精确的都是十几位。
UPD:
有一个结论是单峰函数复合起来还是单峰函数。
UPD:
二维hash。
实在没搞明白它的物理意义,不太像一维$hash$是个$p$进制数。
但打法和二位前缀和的容斥差不多,不过行列的模数不一样。
而且并不知道为何可以用小质数。。。
例题:对称的正方形

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define MAXN 1100 5 #define LL long long 6 #define ull unsigned long long 7 using namespace std; 8 inline int min(int a,int b){return a<b?a:b; } 9 const ull mo1=1e9+7,mo2=72871824517; 10 int n,m; 11 int jz[MAXN][MAXN]; 12 ull sm[4][MAXN][MAXN],bin1[MAXN],bin2[MAXN]; 13 LL ans=0; 14 inline ull cal(int sx,int sy,int bx,int by,int opt){ 15 ull t1=bin1[by-sy+1],t2=bin2[bx-sx+1]; 16 switch(opt){ 17 case 0:return sm[0][bx][by]-sm[0][bx][sy-1]*t1-sm[0][sx-1][by]*t2+sm[0][sx-1][sy-1]*t1*t2;break; 18 case 1:return sm[1][bx][sy]-sm[1][bx][by+1]*t1-sm[1][sx-1][sy]*t2+sm[1][sx-1][by+1]*t1*t2;break; 19 case 2:return sm[2][sx][by]-sm[2][sx][sy-1]*t1-sm[2][bx+1][by]*t2+sm[2][bx+1][sy-1]*t1*t2;break; 20 case 3:return sm[3][sx][sy]-sm[3][sx][by+1]*t1-sm[3][bx+1][sy]*t2+sm[3][bx+1][by+1]*t1*t2;break; 21 } 22 return -1; 23 } 24 void init(){ 25 bin1[0]=bin2[0]=1; 26 for(int i=1;i<=n;++i)bin1[i]=bin1[i-1]*mo1; 27 for(int i=1;i<=m;++i)bin2[i]=bin2[i-1]*mo2; 28 for(int i=1;i<=n;++i) 29 for(int j=1;j<=m;++j) 30 sm[0][i][j]=jz[i][j]+1+sm[0][i-1][j]*mo2+sm[0][i][j-1]*mo1-sm[0][i-1][j-1]*mo1*mo2; 31 for(int i=1;i<=n;++i) 32 for(int j=m;j>=1;--j) 33 sm[1][i][j]=jz[i][j]+1+sm[1][i-1][j]*mo2+sm[1][i][j+1]*mo1-sm[1][i-1][j+1]*mo1*mo2; 34 for(int i=n;i>=1;--i) 35 for(int j=1;j<=m;++j) 36 sm[2][i][j]=jz[i][j]+1+sm[2][i+1][j]*mo2+sm[2][i][j-1]*mo1-sm[2][i+1][j-1]*mo1*mo2; 37 for(int i=n;i>=1;--i) 38 for(int j=m;j>=1;--j) 39 sm[3][i][j]=jz[i][j]+1+sm[3][i+1][j]*mo2+sm[3][i][j+1]*mo1-sm[3][i+1][j+1]*mo1*mo2; 40 return ; 41 } 42 inline bool _judge(int i,int j,int len,int opt){ 43 if(!len)return true; 44 if(opt==1){ 45 ull t1=cal(i-len+1,j-len+1,i,j,0); 46 ull t2=cal(i-len+1,j,i,j+len-1,1); 47 if(t1!=t2)return false; 48 ull t3=cal(i,j-len+1,i+len-1,j,2); 49 if(t1!=t3)return false; 50 ull t4=cal(i,j,i+len-1,j+len-1,3); 51 if(t1!=t4)return false; 52 return true; 53 } 54 else{ 55 ull t1=cal(i-len+1,j-len+1,i,j,0); 56 ull t2=cal(i-len+1,j+1,i,j+len,1); 57 if(t1!=t2)return false; 58 ull t3=cal(i+1,j-len+1,i+len,j,2); 59 if(t1!=t3)return false; 60 ull t4=cal(i+1,j+1,i+len,j+len,3); 61 if(t1!=t4)return false; 62 return true; 63 } 64 return false; 65 } 66 int main(){ 67 //freopen("da.in","r",stdin); 68 69 scanf("%d%d",&n,&m); 70 for(int i=1;i<=n;++i) 71 for(int j=1;j<=m;++j) 72 scanf("%d",&jz[i][j]); 73 init(); 74 for(int i=1;i<=n;++i) 75 for(int j=1;j<=m;++j){ 76 int l=0,r=min(min(i,n-i+1),min(j,m-j+1)); 77 while(r-l>1){ 78 int mid=l+r>>1; 79 if(_judge(i,j,mid,1))l=mid; 80 else r=mid; 81 } 82 if(_judge(i,j,r,1))ans+=r; 83 else ans+=l; 84 } 85 for(int i=1;i<n;++i) 86 for(int j=1;j<m;++j){ 87 int l=0,r=min(min(i,n-i),min(j,m-j)); 88 while(r-l>1){ 89 int mid=l+r>>1; 90 if(_judge(i,j,mid,2))l=mid; 91 else r=mid; 92 } 93 if(_judge(i,j,r,2))ans+=r; 94 else ans+=l; 95 } 96 printf("%lld ",ans); 97 98 return 0; 99 }
UPD:
两个关键字的问题,可以考虑排序其中一个,相当于钦定一个关键字的答案,另一个关键字可以贪心。
那么其实可以说是在有多个限制条件时,考虑是否可以在合法的时间复杂度内枚举(二分)其中的某个,其他限制能简单解决。
UPD:
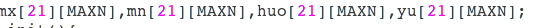
$\%\%$$fh$大神
尽量把维度小的放在前面,原理是:尽管数组访问是$O(1)$的,但如果访问$f[x][j-1]$和$f[y][j-1]$时,会先在$x$里找,再去$y$,如果把第二维放前面,就能保证询问的连续性,从而节省时间。
UPD:
时间戳代替bool数组清空的思想应该仔细研究
一个数组的时间戳不一定要表示成状态是否为当前状态,可以表示成是否当前合法。
那么不为当前的时间戳的,要么原来就不合法,要么之前合法,但当前不合法。
UPD:
字符串不能读入空格
UPD:

$lucas$也用作$(n,m)$范围大的时候
UPD:
概率与期望,现在只能背了,证明都不太会

UPD:
向上取整:
$ceil((double)x)$
UPD:
小于$1e9$的数的约数个数最大为$1344$
UPD:
$2e8$能筛出$1e7$多个素数
